Online since 2002. The most comprehensive site for all around twisty puzzles.
|
Member Collections > chbouchard777 - My Collection
2X2X2
3X3X3
4X4X4
5X5X5
CUBE (SHAPE PRESERVING)
CUBE (SHAPE CHANGING)
 Get back to Square-1
Quantity: 1
An american based version of the Square-1. It distinguishes itself from the other variants because it was sold in scrambled state.
Get back to Square-1
Quantity: 1
An american based version of the Square-1. It distinguishes itself from the other variants because it was sold in scrambled state.
FOUR
CYLINDER
HEADS & OBJECTS
SIAMESE & FUSED
FOLDING
OTHER MECHANISMS
MECHANISM PICTURES
UNKNOWN
 Rubik's Magic
Quantity: 0
The newest version produced by Rubiks.com and has brighter colours (nicknamed by the record holders)
Rubik's Magic
Quantity: 0
The newest version produced by Rubiks.com and has brighter colours (nicknamed by the record holders)
|
|
 Harry Potter
Harry Potter
 Rubik's Mini Cube
Rubik's Mini Cube
 Rubik's Cube (OddzOn)
Rubik's Cube (OddzOn)
 Rubik's Cube Key Ring
Rubik's Cube Key Ring
 Rubik's Revenge (OddZon)
Rubik's Revenge (OddZon)
 Rubik's 5x5x5
Rubik's 5x5x5
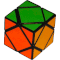 Skewb
Skewb
 Pyraminx (Meffert 1981)
Pyraminx (Meffert 1981)
 Bump Cheese
Bump Cheese
 Homer Simpson Head
Homer Simpson Head
 Siamese 3 (1x1x3)
Siamese 3 (1x1x3)
 Harry Potter Magic
Harry Potter Magic
 Rubik's Magic (OddzOn)
Rubik's Magic (OddzOn)
 Rubik's Master Magic
Rubik's Master Magic
 Rubik's Snake
Rubik's Snake
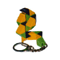 Rubik's Snake Keychain
Rubik's Snake Keychain
 Super Master Magic 'Magic Balls'
Super Master Magic 'Magic Balls'
 Rubik's Clock
Rubik's Clock
 4x4x4 Mechanism
4x4x4 Mechanism
 5x5x5 Mechanism
5x5x5 Mechanism
 Rubik's Cube Mechanism
Rubik's Cube Mechanism