|
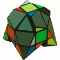
A 3x3x3 half-regularly truncated 12 times on the corners. The result is similar to the Half-Truncated-Cube.
This puzzle is part of the series "Sharp Corners". All modifications of this series are made by truncating an 3x3x3 on its corners. These truncations are not regular as in the Half Truncated Cube. One dimension of the cut goes deeper than the other two. This half-regular style of truncating a corner was popularized by the Hexagonal Dipyramid. The cutting depths do have to go as deep as in the Hexagonal Dipyramid. The Triakis Tetrahedron is another example which uses half-regularly truncated corners too but with diffrent cutting depths. This modification resembles the half truncated cube as four diagonals between two corners still have their original length. Would anyone extend the sides remaining from the original the result would be a solid very similar to the "Pyramorphinx" (see the slight difference in name compared with the Pyramorphix) from Mefferts, a 3x3x3 in shape of a Reuleaux tetrahedron. The puzzle was mass produced by Mefferts under the title "aXe". In 2009 Kyler van der Gaag created a very similar version of this puzzle but deeper truncated and gave it the name "Tetra Pyramid DC". See image 4.
Contributors
Thank you to the following people for their assistance in helping collect the information on this page: Andreas Nortmann, Matt. Collections This puzzle can be found in collections of these members: Cubrick: Cubrick's collection proprin: Prin's collection lunny: Lunny's Collection Nestor: White & primary ONLY collection technoloko: Technoloko's chewbacca: Chewbacca's Collection Novus: My Twisty Obsession dzhoshi: My collection kbloise318: Bloise's Twisty Puzzle Collection matthewdgibbs: Matthew's Collection TylerMcDaniels: Tyler's Collection kasmca: Kasmca's Puzzle Collection gramotej: My growing collection mArtorell: My Collection Shell Snair: Shell's Collection (Maintenance in Progress) fbgrac: Bini's Collection Trung Dung: Trung Dung small collection MartinB: MY COLLECTION MODSDESIGNMB Nazhan94: My Escapism Collection jammytea: Jammytea's collection jackmarcusdeayala: JMDA Collection SGCuber: Sean's Collection LinerPZ: Emil's Collection thecustomcuber: Custom Cuber Collection (Updating) mosaltzevandrey: Andrey's collection Found a mistake or something missing? Edit it yourself or contact the moderator. |
|