|
Puzzles Designed And Made By Jürgen Brandt
by Geert Hellings, photo editing by Wayne Johnson
Introduction
Occasionally, he uses wood. For filling holes, Jürgen uses a material called "Keraquick", a non-toxic ceramic powder that can be mixed with water.
Face-Turning Octahedron
The first, or at least one of the first puzzles Jürgen made, was a so-called "Face-turning Octahedron".
Each "face" consists of 4 pieces, the 3 turning edge parts and a centre part. The centre parts are attached by means of long screws and via hollow rods onto an octahedron centre core made from "filled" cardboard. The moving sides are attached to the centre parts by means of small lids.
The entire puzzle moves reasonably well as long as not too large forces are applied onto the (moving) parts. Another easier way of making a "Face-turned Octahedron" is to make use of a "Rainbow cube" and attach small pointed pieces onto each of the square faces of the "Rainbow cube", as is illustrated below, of cardboard pieces.
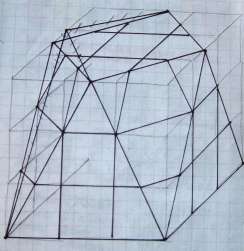
Face-Turning Icosahedron
In a similar way as the "Face-turning Octahedron" Jürgen has also made a "Face-turning Icosahedron". The puzzle is made using a centre "Dodecahedron" shaped core, hollow distance rods, screws (all "inside") and the centre pieces and turning pieces on the outside of the puzzle. The puzzle can be played with, but due to the large openings on the inside it has to be used rather carefully.
Edges Only Cube
Quite another kind of puzzle that Jürgen invented is the so-called "Edges only" cube.
The puzzle has many hollow areas allowing 4 edges to move simultaneously. The core of the puzzle is a regular 333 cube. The corners are largely truncated (these are not "functional" and should allow the edge pieces to move "inside" the puzzle). The edge pieces consist of thin material (e.g. 1 mm) attached to each of the 12 edge pieces of the 333 cube. The puzzle is not very difficult to solve, but has a nice appearance. It is very special in the sense that certain pieces move underneath neighbouring pieces.
Edge Dodecahedron
In the same way as with the "Edges Only" cube also a "Megaminx" can be turned into an "Edge" puzzle by largely truncating the 20 corners and adding thin materials to the 30 edges. (No illustrations supplied)
Pyraminx Variations
Jürgen has made several Pyraminx-variations by truncating Pyraminx puzzles in a very clever way. Some of these variations were also already shown on the website of Hendrik Haak. a. The first variation is a puzzle for which the 4 trivial tops are removed after which each of the 6 edges of the Pyraminx is truncated for half of a piece.
b. A second variation is found by a further truncation of this puzzle along the 6 edges. See the figures below for a comparison of these 2 puzzles.
c. A third kind of truncation is shown below.
This time only 3 edges are truncated. It starts with removing one of the trivial tops and by drawing a regular hexagon on the appearing triangular top. Next the 3 adjacent edges are truncated:
This also "removes" the other 3 trivial tops. d. Working out the idea above in 4 directions yields the puzzle which Jürgen calls "Knuffy"(Figures 25-28).
e. Yet another way of truncating the Pyraminx according to the way as shown:
yields the puzzle as shown here:
f. Probably the most difficult truncation of the Pyraminx that Jürgen has made is the "Icosahedron from Pyraminx":
3x3x3 Cube Variations
One of the interesting 333-cube variations that Jürgen made is a further truncation of the 14-sided cube or "Cuboctahedron" cube. Further truncation of the 8 corners of this puzzle yields the following:
Another idea of Jürgen's that has not yet materialised in a puzzle is the truncation as sketched in the following figure:
A third cube-variation is a puzzle that Jürgen calls the X-cube.
Jürgen has made the puzzle by means of 12 V-shaped grooves at all 12 edges of the puzzle. Also the corner parts are slightly adapted. Megaminx Variations
The principle of the X-cube can also be applied to a "Megaminx", yielding this puzzle:
This is not the first Megaminx-variation that Jürgen has made. Well-known is his "Megaminx-ball".
The "Megaminx-ball" is a Megaminx for which the corners and edges have been truncated. Adapting the edges to have these "matched" again with the corner pieces yields the rectangular shape for the edges. Raising these adapted edge-pieces slightly results in the puzzle as:
Adding slightly longer, adapted pieces to the edge pieces as well as adding "tops" to the "pentagon" shaped pieces of the Megaminx results in the "Icosahedron from Megaminx":
Jürgen also adapted his "Megaminx-ball" in a truly ball-shaped, almost fully round puzzle: Jürgen managed to obtain the round shape by turning the puzzle inside a cone covered at the inside with sand-paper:
Other Megaminx variations of Jürgen's involve his cube-approach of the Megaminx:
An "irregular" truncation of the Megaminx:
Octahedron from a 4x4x4
One of the most interesting puzzles Jürgen made is the Octahedron from 4x4x4:
Jürgen made a prototype using various kinds of materials. He started by truncating a 444 cube:
The following figure 57 shows the triangular pieces:
In addition, small pieces are made:
These are added to the side pieces of the truncated 4x4x4 cube:
Next the additions are made that are to be attached to the centre pieces of the 4x4x4. The following figures show how the puzzle is assembled:
Variations from a 5x5x5
Lastly, Jürgen also has made some variations on 5x5x5 puzzles. Just as an example the "Cuboctahedron" puzzle he made from a 5x5x5:
|
|

 Jürgen Brandt is 43 years old, single and living in Worms in Germany.He started puzzle-making and collecting in 1998 resulting from a general interest in polyhedra. When Jürgen is designing and making a new puzzle he often first makes a model using a particular kind of cardboard-paper. The origin of this cardboard paper is (plastified) "milk-carton". The inside of this material has a nice, rather shiny surface.The "cardboard" pieces are cut and glued together using transparent tape. This is a very fast and effective way of working. For some other pieces that do not require much thickness, Jürgen applies a 3 mm thick material called "Hartschaumplatte" which is relatively easy to work with.
Jürgen Brandt is 43 years old, single and living in Worms in Germany.He started puzzle-making and collecting in 1998 resulting from a general interest in polyhedra. When Jürgen is designing and making a new puzzle he often first makes a model using a particular kind of cardboard-paper. The origin of this cardboard paper is (plastified) "milk-carton". The inside of this material has a nice, rather shiny surface.The "cardboard" pieces are cut and glued together using transparent tape. This is a very fast and effective way of working. For some other pieces that do not require much thickness, Jürgen applies a 3 mm thick material called "Hartschaumplatte" which is relatively easy to work with.