Today, twisty puzzles are more popular than ever. Companies like Chronos, Mefferts, Cube4You and MF8 are bringing out many new twisty puzzles, some of which only remotely resemble the Rubik's Cube [1]. The Twisty Puzzles Forum [2] has becoming a large source of innovations. Twisty puzzle enthusiasts, some as young as 12 years, design and build novel twisty puzzles to show and sell to their friends. This article is about a particular innovation, namely "jumbling", and some Oskar-Bram collaborations in this area.
Bevel Cube / Helicopter Cube
The concept of "jumbling" was first recognized in the Bevel Cube [3] / Helicopter Cube [4], which were independently invented and developed by Okamoto and Cowan. Figure 1 shows that there is something unusual about this puzzle. At first, it looks like an ordinary twisty puzzle, with twelve edges each turning by multiples of 180 degrees. But when one edge is turned by 70.5 degrees, then adjacent edges can turn too. The result is a scrambled puzzle that is no longer a cube and with some of the edge rotations are blocked. Adam Cowan called it "jumbling" [4].
Figure 1: Jumbling of the Bevel Cube / Helicopter Cube.
Definition of jumbling
Bram provided a mathematical definition for jumbling [5], which had been refined over several discussions with other twisty-puzzle people.
Definition: A twisty puzzle "jumbles" when it cannot be unbandaged into a doctrinaire puzzle.
This definition uses some terms that require further explanation. The term "doctrinaire" refers to a (classic) twisty puzzle that returns to the same three-dimensional shape after each turn. The Rubik's Cube is a doctrinaire puzzle. After each turn, it is the same cube, except for the sticker locations. Engel's Enigma [6], a flat equivalent of Rubik's Cube, is also a doctrinaire twisty puzzle, see Figure 2.
Figure 2: Rubik's Cube and Engel's Enigma are doctrinaire twisty puzzles.
Some twisty puzzle designers specialize in "modding" of twisty puzzles by cutting off corners or adding extensions. A famous example is the Fisher Cube [7], see Figure 3. Mathematically it turns like a (doctrinaire) Rubik's Cube.
Figure 3: The Fisher Cube is a shape mod of the Rubik's Cube.
"Unbandaging" is the next term from the definition. Bandaging of a twisty puzzle is achieved by gluing adjacent pieces together. Bicube [8] is a bandaged Rubik's Cube. The bandaging block some rotations, so a completely new solving strategy has to be found. Bandaging typically makes as twisty puzzle harder to solve. Rotascope [9] is a flat bandaged twisty puzzle. Unbandaging is the reverse act of bandaging. In case of the Bicube, it would be cutting the glue joints and stickers to turn it back into the original Rubik's Cube. So following Bram's definition, Bicube does not jumble because it can be unbandaged into a doctrinaire twisty puzzle. Neither does Rotascope.
Figure 4: Bicube and Rotascope are bandaged twisty puzzles.
The core part of the definition is "cannot be unbandaged". Figure 5 shows a simple flat twisty puzzle and some vain attempts to unbandaged it. Step 1 shows the start position. After two moves, the left circle is blocked. By cutting two pieces ("unbandaging"), the left circle can turn again. But when turning it, the right circle is blocked. After some more cutting the right circle can turn again, but now the left circle is blocked. More cutting to do. The result is a never ending process of turning and cutting, ultimately cutting the puzzle to dust. It may be clear that this puzzle cannot be unbandaged into a doctrinaire puzzle, so it jumbles.
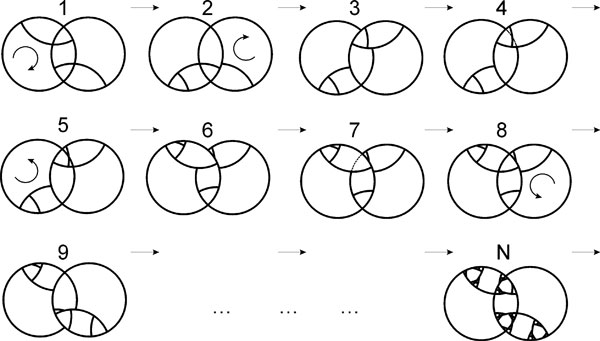Figure 5: Vain attempts to "unbandage" a simple flat twisty puzzle.
Figure 6 shows that the underlying geometry of the Bevel Cube / Helicopter Cube. The unbandaging process would be similar to that of the flat example, ultimately turning the puzzle to dust.
Figure 6: Geometry of the Bevel Cube / Helicopter Cube.
More jumbling puzzles
This section will discuss some more jumbling twisty puzzles that have been published recently. Doug Engel's Binary Bisect 5 is an elegant flat example, see Figure 7. We leave it to the reader to demonstrate or prove that this puzzle jumbles.
Figure 7: Binary Bisect 5 jumbles.
Bram came up with the Jumble Prism, which was designed in 3D by Oskar and prototyped by George Miller. It is based on the geometry of a triangular prism. Now understand the concept of jumbling, Oskar designed and prototyped [11] several more jumbling puzzles: Meteor Madness (geometry of Triangular Dipyramid), Astroid Attack (geometry of Tetragonal Trapezohedron), Crazy Comet (geometry of Rhombic Dodecahedron) and Big Boulder (geometry of Pentagonal Hexecontahedron). The latter puzzle has 60 turning centers, 140 corners and 150 edges.
Figure 8: Jumble Prism, a jumbling puzzle based on a triangular prism.
Figure 9: Meteor Madness, Astroid Attack, Crazy Comet and Big Boulder all jumble.
Bram and Oskar created Uncanny Cube and Canny Uncube, see Figure 10, which look much more regular than the previous puzzles, but they still jumble by definition. Analysis by Bram showed that also Sergsey Makarov's Hedgehog Cube (1984 [11], re-created by Oskar as Mixup Cube [see footnote 1] in 2009) jumbles. A new "regular" jumbling puzzle is Oskar's Mixup 2x4x4 [11].
Figure 10: Also Uncanny Cube, Canny Uncube, Mixup Cube and Mixup 2x4x4 jumble.
Oskar discovered that regular geometry is not required for jumbling. In 2009, he designed and built Fairly Twisted [11], a jumbling twisty puzzle with some local five-fold, four-fold and three-fold symmetries, but no overall symmetry. The puzzle has seven turning centers, 11 edges and 17 corners, which all are prime numbers. Another irregular jumbling puzzle is Oskar's Distorted Cube [11], which looks like a Rubik's Cube that has melted in an oven. Four of the faces turn like a "regular" jumbling twisty puzzle. A bit of "fudging" was needed to make the other two faces turn, but that is another story.
Figure 11: Fairly Twisted and Distorted Cube have no regular geometry.
Conclusion
Jumbling is an exciting new concept for twisty puzzles. It has a clear definition that distinguishes it from shape mods and bandaged twisty puzzles. Recently, many new jumbling puzzles have been invented and built, and there may be many more to come.
Footnotes
- Whether Mixup Cube jumbles is open to debate. Bram considers it a shape mod of a doctrinaire puzzle, whereas Oskar sees opportunities for unbandaging when a single face is turned by 45 degrees.
References
- Jerry Slocum, David Singmaster, Dieter Gebhardt, Geert Hellings, Wei - Hwa Huang,"The Cube: The Ultimate Guide to the World's Best-selling Puzzle: Secrets, Stories, Solutions", http://search.barnesandnoble.com/The-Cube/Jerry-Slocum/e/9781579128050, 2009
- Sandy Thompson, "Twisty Puzzles Forum", http://twistypuzzles.com/forum/
- Katsuhiko Okamoto, "Bevel Cube", http://www.puzzleworld.org/DesignCompetition/2007/, 2007
- Adam Cowan, "Helicopter Cube", http://twistypuzzles.com/forum/viewtopic.php?f=9&t=6253, 2007.
- Bram Cohen, "To jumble or not to jumble", Tech Shop talk, http://www.youtube.com/watch?v=3hOttwmlmSE, http://www.youtube.com/watch?v=ki_pdcIIQzM, 8 August 2009.
- Douglas Engel, Engel's Enigma, US patent US 4 415 158, http://v3.espacenet.com/publicationDetails/biblio?CC=US&NR=4415158A&KC=A&FT=D&date=19831115&DB=EPODOC&locale=en_EP, 1983.
- Tony Fisher, "Fisher Cube", http://tonyfisherpuzzles.net/, 1985.
- Jaap Scherphuis, "Bicube" (inventor unknown), http://www.jaapsch.net/puzzles/bandage.htm
- Jaap Scherphuis, "Pentangle's Rotascope" (inventor unknown), http://www.jaapsch.net/puzzles/rotascope.htm
- Douglas Engel, "PuzzleAtomic", http://www.puzzleatomic.com/
- Oskar van Deventer, "OskarPuzzles", http://www.shapeways.com/shops/oskarpuzzles, 2009-2010
- Sergey Makarov, "Hedgehog Cube", http://v3.espacenet.com/publicationDetails/biblio?CC=SU&NR=1191088&KC=&FT=E, 1984.
