|
Tony Fisher's Cuboid 3x3x3 Transformations
by Dieter Gebhardt
(Permission to reproduce this article was granted to TwistyMegasite.com by the editorial board of CFF, Dieter Gebhardt and Tony Fisher.)
Introduction
Like myriads of other people I have been fascinated by Rubik's cube and like many of these I have been fanatically collecting all the different designs. The cover of the Silver CFF (CFF 25) has been decorated by a colour photo with 25 cubes from Edward Hordern's collection: the same basic puzzle embellished with stickers of different motifs. I remember going in childlike joy through the pictures showing flowers and fruits, Santa Claus with his gifts and Mickey Mouse with his companions, girls and butterflies, traffic signs and animals (one big or also nine small on each side). There were cubes with playing-card symbols and magic squares, advertising cubes and others. I have quite a few of them in my collection and have been enjoying them eminently. 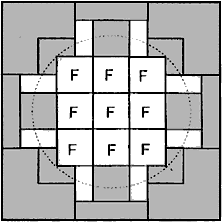 Fig. 1: Frontal aspect of open maxi cube. F marks the fully visible front of the kernel.
Fig. 1: Frontal aspect of open maxi cube. F marks the fully visible front of the kernel.
The mystery seems to be solved now. Soon after the appearance of Rubik's cube, Tony Fisher had made a 3x3x3 maxi cube from a normal one by trickily extending the rotating mechanism. You will see that the maxi 3x3x3 is not a marginal item for cube freaks' collections but the starting point for the understanding of a series of perplexing cuboid transformations.
The 3x3x3 Maxi Cube and Micro Cube
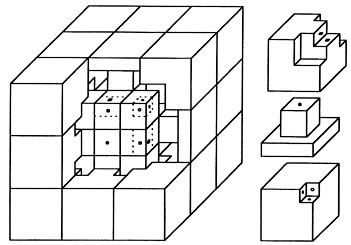 Fig. 2: Cut away view of 3x3x3 maxi cube with Rubik's cube kernel.
Fig. 2: Cut away view of 3x3x3 maxi cube with Rubik's cube kernel.
The linear dimensions of the 3x3x3 maxi cube are about twice as large as those of Rubik's cube. In general, any side length (larger than that of the cube kernel) is possible. Looking at figures 1 and 2 you will surmise problems with attaching the additional corner pieces when the side length of the maxi cube gets too large. Of course, they could be fixed in this case to the corner pieces of the 3x3x3 kernel by a suitable connecting rod. But one can also make a stable macro cube by simply applying the standard to maxi transformation concept according to Figure 1 to the maxi cube which in combination results in a stable standard to maxi to macro transformation. If you are such an inconvertible cube addict as I am you may say, "fine trick, professional realisation and pretty product, but a rotating 3x3x3 cube I have had for almost twenty years. So what?" The point is the following: Tony used the above one together with another basic trick to make also a 3x3x2 and a 2x2x3 from a Rubik's cube. Do you have any idea how to get along with this problem? And the story goes on: even these cube transformation are only the predecessors of more perplexing puzzles that will be described in a future part of this series of CFF articles on Tony Fisher's marvellous creations.
3x3x2 Rotating Puzzles
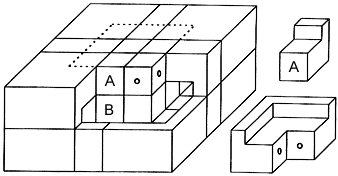 Fig. 3: Cut away view of 2x3x3 puzzle with Rubik's Cube kernel.
Fig. 3: Cut away view of 2x3x3 puzzle with Rubik's Cube kernel.
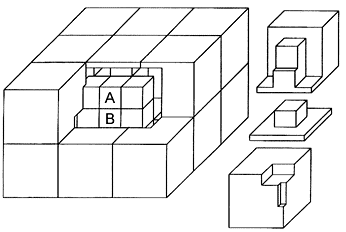 Fig. 4: Cut away view of 2x3x3 cuboid Puzzle with Rubik's Cube kernel.
Fig. 4: Cut away view of 2x3x3 cuboid Puzzle with Rubik's Cube kernel.
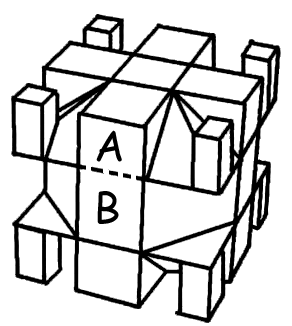 Fig. 4b: The above illustration drawn by Joshua Bell is the required kernel to make the 3x3x2 if using a keychain and regular sized cubes together.
Fig. 4b: The above illustration drawn by Joshua Bell is the required kernel to make the 3x3x2 if using a keychain and regular sized cubes together.
Tony found an impressive solution to the problem: omit two parallel cutting planes of the 3x3x3 kernel and replace them in a symmetrical way by one new (outside) cutting plane midway between them. A possible realisation is shown in Figure 3. Only one horizontal cutting plane is left in the outer envelope of the puzzle. The basic turns of the upward and downward outer face apparently are by multiples of 90 degrees, those of the right, front, left and back face only by multiples of 180 degrees. The edge cubelet A of the upward layer of Rubik's cube has to be glued to the neighbouring centre cubelet B (see Figure 3). The reason is a simple one. When you turn a face of your standard Rubik's cube you hold the cube in such a way that the two remaining layers are not shifted against each other. Otherwise the continuation would be blocked. The 3x3x2 puzzle from Figure 3 in its completed state has the horizontal middle layer of the cube unapproachable inside the puzzle. To avoid the possible blocking of sequential moves, cubelets A and B are tightly connected. By this, a turn of the upward against the downward outer face of the 3x3x2 puzzle always corresponds to a turn in either the upper or the lower horizontal cutting plane of the hidden Rubik's cube. Unfortunately the puzzle from Figure 3 is not yet proportionate, that means the visible parts are not cubelets. This disturbed Tony's feelings for puzzle aesthetics and he settled this by (besides the cutting planes trick just explained) additionally applying the (suitably modified) transformation procedure from the preceding section. The result is a cuboid 3x3x2 puzzle that is shown in Figure 4. With reference to figures 1 to 3 and the corresponding explanation the matter might be evident. It should be mentioned that in the early eighties there was a 3x3x2 cuboid puzzle from industrial production. It was offered with the cubelets having the size of those of Rubik's cube and because of its pertinent design it was called Magic Domino. There were also smaller versions with Santa Claus and with Superman motifs. All of these had a rotating mechanism of very bad quality.
The 2x2x3 Cuboid Puzzle
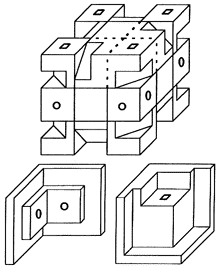 Fig. 5: Composition plan for a 2x2x3 cuboid puzzle from Rubik's Cube.
Fig. 5: Composition plan for a 2x2x3 cuboid puzzle from Rubik's Cube.
Another aspect appears here. Above the size of the transformations was chosen in such a way that the basic ideas could be explained step by step. Tony's realisation takes account of another point. He wanted to make all these kxlxm puzzles from the high quality rotating mechanism of the 57 mm standard cube with uniform (and not unnecessarily large) size for the cubelets. For this he applied a further idea, namely to suitable cut down the extension of the 3x3x3 kernel. Figure 5 shows the final design for the 2x2x3 cubic puzzle from the master's hand. The incisions into the Rubik's cube do not cause any trouble. To see this one only has to consider the well known transformations of a cube into an octagonal prism and a cube without corners. Four cubelets in the upper layer are glued together. Uncontrollable shifts of hidden middle layers of the Rubik's cube inside the completed 2x2x3 puzzle are avoided by this. Without the introductory comments from the above sections, Figure 5 would not be readily understood at all. Remember the reason: There are three different aspects involved. First the cutting planes trick, second the all-cubelets-of-the-same-size concept and third the size adapting finish.
Conclusion
You surely are aware that by the above concepts also a 2x2x2 cube could be made from a 3x3x3. Most of you, before reading this article, might have said what I did earlier: I do not know how this should work. In fact, the series of Tony's cuboid kxlxm puzzles includes a 2x2x2 maxi cube but this is simply based on a 2x2x2 kernel. It might be considered as the starting point for Tony's cuboid transformations. The general direction of the future continuation of this article is uphill of course instead of downstairs. Let us see where that leads.
Editor's Notes
by Wayne Johnson
Have fun.
|
|
 Just thought I'd tack some thoughts on here. So does it work? Yes it does. I have built the following working 2x2x3 puzzle and it moves beautifully, even when using cheap cubes and doing the job very roughly. a 2x2x3 is not an easy puzzle either, might I add. It's the cousin of the Domino, but I would say that I am finding this puzzle a little tougher than the Domino due to it's obvious restrictions.
Just thought I'd tack some thoughts on here. So does it work? Yes it does. I have built the following working 2x2x3 puzzle and it moves beautifully, even when using cheap cubes and doing the job very roughly. a 2x2x3 is not an easy puzzle either, might I add. It's the cousin of the Domino, but I would say that I am finding this puzzle a little tougher than the Domino due to it's obvious restrictions.