|
2x2x4 And 2x2x6 Cuboid Modifications
by Geert Hellings
A Fully Operational 2x2x4 Cube with Uniform Cubies
I have made such a fully functional 2x2x4 puzzle of the same size in a slightly different way. As a basis I have used a regular (Rubik's "Revenge" type) 4x4x4 cube. As a next step, 8 (2x2x2)-cubies can be added to the 8 centre pieces of two opposite faces. Evidently this does not result in a functionally working 2x2x4 puzzle since rotational movements of the 4 centre pieces will be blocked within the plane of the 12 surrounding edge and corner pieces. To overcome this, I have first rounded and truncated the centre pieces in such a way that a set of 4 centre pieces can rotate freely within the plane of the surrounding 12 pieces. Adding now the 8 (2x2x2)-cubies to the 8 truncated centre pieces will result in a real 2x4x4 cube with cubies of size "2". A first fully working prototype has been made.
Rotating the pieces of this 2x2x4 prototype results in some nice shape variations.
The 8, 16 or 24 pieces added in this way all have a "double size" (2x2x2) compared to the cubies of the regular 4x4x4. Adding 32 non-uniform "cubies" of dimensions 1x2x2 in 8 stacks of 4 "cubies" another "cross"-shaped puzzle (of height "4") can be formed. A "schematic" top-view of this 4-layered puzzle will again look like the cross-shaped figure below. Moreover, the same principle can be used to create 6-layered puzzles, which I will illustrate next.....
The First Fully Operational 6-Layered Cube
Well, to be honest, it is not a full 6x6x6 cube in all directions, but it certainly is a fully functioning, operational 6-layered puzzle that allows full interchangeability of (corresponding) parts. Using the same principle as for the "2x2x4" cube with uniform (2x2x2)-"cubies" (see above), I have added 8 non-uniform 1x2x2 "cubies" to the 8 centre pieces of two opposite planes of a regular 4x4x4 cube. Prior to this the centre pieces have been truncated in the same way as for the 2x2x4 cube, allowing rotation of 2 sets of these 4 centre pieces within the plane of their 12 surrounding pieces (8 edge pieces and 4 corner pieces). The result is a 2x2x6 cube. A first fully operational prototype has been built. Clearly a 2x2x5 variation can easily be made in the same way. To my knowledge it is the first operational "cube" with dimension 6!! Non-trivial "cube"-type puzzles with 6 layers (or even more layers) have been made before by adding non-movable pieces or in the case of "siamese" cubes. However, in those cases, parts from e.g. the top half of the puzzle can not be exchanged with parts of the lower half of the puzzle. In contrary, the puzzle presented here is fully 6-layer operational in the sense that all "cubies" can be interchanged with corresponding "cubies" at both sides of the puzzle.
A 6-Layered "Cube" in 3 Dimensions
In the case of the 2x2x6 puzzle, the principle of creating a 6-layered puzzle is applied in one dimension. However, the same principle can also be applied in 2 or 3 dimensions. Applying it to 3 dimensions requires all 24 centre pieces to be adapted as described above. Next, 24 cubies of unit size "1" can be added to these centre pieces. Please note that the 24 added pieces of this puzzle can all be rotated and can all be exchanged with one another. The puzzle basically can be regarded as a 6x6x6 puzzle in 3 dimensions, although with "truncated" (eliminated) edge parts.
How to Prepare the Parts
For each of the three different types of puzzles described above the 4 centre pieces have to be adapted/truncated in the same way, such that the edge pieces and the centre pieces can easily be rotated with respect to each other.
Evidently the L-shaped part that fits inside the ball-shaped internal mechanism of the puzzle has to remain unaffected.
Next the pieces are coloured and stickers are attached...
The pieces made in this way can easily be assembled into the puzzle. Preferably the largest pieces are assembled first.
Geert Hellings |
|
 Already some time ago 2x2x4 cubes were proposed and made by a kind of bandaging of a 4x4x4 cube, resulting in non-uniform "cubies" of size 1x2x2. Tony Fisher probably was the first to make a 2x2x4 "cube" with "cubies" having uniform sizes for all sides. His ideas are presented by Dieter Gebhardt in CFF (Cubism For Fun) number 49 of June 1999. The size of the "cubies" of Tony's 2x2x4 are 3 times the size of the "cubies" of the regular 4x4x4. Wayne Johnson recently also presented an internal mechanism (prototype completed) for a 2x2x4 with cubies having uniform sizes for all sides and with cubies the same size as those on the standard 2x2x2.
Already some time ago 2x2x4 cubes were proposed and made by a kind of bandaging of a 4x4x4 cube, resulting in non-uniform "cubies" of size 1x2x2. Tony Fisher probably was the first to make a 2x2x4 "cube" with "cubies" having uniform sizes for all sides. His ideas are presented by Dieter Gebhardt in CFF (Cubism For Fun) number 49 of June 1999. The size of the "cubies" of Tony's 2x2x4 are 3 times the size of the "cubies" of the regular 4x4x4. Wayne Johnson recently also presented an internal mechanism (prototype completed) for a 2x2x4 with cubies having uniform sizes for all sides and with cubies the same size as those on the standard 2x2x2.







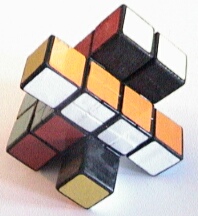
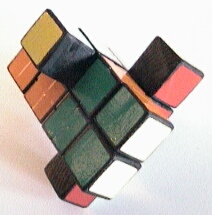
 Evidently, the same principle can be extended to two or three dimensions by adding 16 or 24 (2x2x2)-cubies to a 4x4x4 puzzle with adapted centre pieces. Adding 16 pieces creates the shape of a cross (see below for a "schematic" side-view). Adding 24 pieces creates the shape of the so-called "Hexcross"-puzzle, however, now with the possibility of rotating and exchanging all added parts (the original "Hexcross"-puzzle is a 2x2x2 with attached, non-movable pieces).
Evidently, the same principle can be extended to two or three dimensions by adding 16 or 24 (2x2x2)-cubies to a 4x4x4 puzzle with adapted centre pieces. Adding 16 pieces creates the shape of a cross (see below for a "schematic" side-view). Adding 24 pieces creates the shape of the so-called "Hexcross"-puzzle, however, now with the possibility of rotating and exchanging all added parts (the original "Hexcross"-puzzle is a 2x2x2 with attached, non-movable pieces).






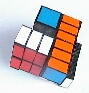




 The basic principle of preparing the parts starts with a regular 4x4x4 Rubik's revenge puzzle of the "old" type. Unfortunately the very nice new 4x4x4 cubes of size 60 mm cannot be adapted in the same way since the internal mechanism is different.
The basic principle of preparing the parts starts with a regular 4x4x4 Rubik's revenge puzzle of the "old" type. Unfortunately the very nice new 4x4x4 cubes of size 60 mm cannot be adapted in the same way since the internal mechanism is different.

 Looking from underneath a set of 4 edge pieces , it can be observed that, in order to allow the rotation of the pieces, all 4 edges of both the "outer" square as well as the "inner" square have to be trimmed/lowered.
Looking from underneath a set of 4 edge pieces , it can be observed that, in order to allow the rotation of the pieces, all 4 edges of both the "outer" square as well as the "inner" square have to be trimmed/lowered.

 Using a simple handsaw, this can easily be done by sawing parallel to the plane approximately half-way the thickest part of the centre pieces.
Using a simple handsaw, this can easily be done by sawing parallel to the plane approximately half-way the thickest part of the centre pieces.


 Next the pieces are rounded:
Next the pieces are rounded:
 And (using super-glue) glued to "cubies" of size 2x2x2 for the 2x2x4 puzzle.
And (using super-glue) glued to "cubies" of size 2x2x2 for the 2x2x4 puzzle.
 And glued to "cubies" of size 1x2x2 for the 2x2x6 puzzle.
And glued to "cubies" of size 1x2x2 for the 2x2x6 puzzle.
 Or glued to "cubies" of size 1x1x1 for the 6 layered puzzle in 3 dimensions.
I have used wooden blocks for this, but evidently other materials can be used as well.
Or glued to "cubies" of size 1x1x1 for the 6 layered puzzle in 3 dimensions.
I have used wooden blocks for this, but evidently other materials can be used as well.





